|
 |
 |
 |
 |
 |
חזרה3 |
הדוגמא המוקדמת ביותר למערכת מספרים אדיטיבית היא מערכת המספרים שהתפתחה במצרים העתיקה ב- 3500 לפנה"ס, ואיפשרה למנות מספרים גדולים ככל שנרצה, עם הוספה של סימן בסיסי מדי פעם.
כתב החרטומים המצרי, הכתב ההירוגליפי, הינו כתב ציורי, שבו כל אות מייצגת עצם כלשהו במציאות. ולכן גם המספרים בכתב המצרי מיוצגים ע"י ציורים של עצמים שונים.
מערכת המספרים המצרית מבוססת על השיטה העשרונית (כלומר בסיס הספירה הוא 10), ולכן הסימנים הבסיסיים שמוגדרים בה הם עבור מספרים שהם חזקות של 10. בסיס הספירה 10 נחשב לבסיס ה"טבעי" והוא היה נפוץ במערכות מספרים קדומות, עקב השימוש שנעשה בעשר האצבעות כדי לספור עצמים שונים.
מערכת המספרים המצרית מוצגת באיור הבא:
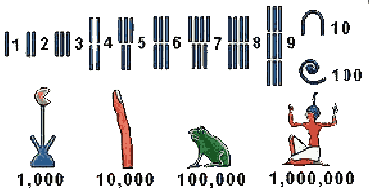
כפי שניתן לראות, למצרים היו סימנים מיוחדים ליחידה ולחזקות שונות של 10. המספר 1 מיוצג ע"י סימן של מקל אנכי. סימן זה דומה לסימן 1 שלנו, והוא היה מקובל כמעט בכל מערכות המספרים הקדומות לייצוג המספר 1 (כנראה שמקורו בצורה של אצבע מורמת ששימשה לספירה). המספר 10 מיוצג ע"י צורה של פרסה, והוא מחליף רישום של 10 מקלות נפרדים.
100 מיוצג ע"י חבל מעוקל או מגילה, 1,000 מיוצג ע"י פרח הלוטוס, 10,000 מיוצג ע"י אצבע מצביעה, 100,000 מיוצג ע"י צפרדע, ו- 1,000,000 מיוצג ע"י אדם כורע המרים את ידיו בהשתאות.
מספרים אחרים נכתבו ע"י שילוב של הסימנים האלה בצורה חיבורית, כלומר הערך של המספר הנכתב ע"י שילוב של הסימנים הבסיסיים שווה לסכום המספרים המיוצגים ע"י הסימנים האלה, כאשר לא חוזרים על אותו סימן יותר מ- 9 פעמים.
לדוגמא נסתכל על המספרים הבאים:
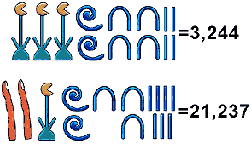
בשיטת הכתיבה החיבורית אין חשיבות לסדר של הסימנים במספר, ואכן לעיתים הסימנים בעלי הערך הגבוה יותר היו נכתבים דווקא בצד ימין. בניגוד למערכת המספרים שנהוגה כיום, שיטת כתיבת המספרים המצרית לא הייתה פוזיציונלית (מיקומית) – שיטה שבה לסימן מסוים יש משמעות שונה בהתאם למיקום שלו במספר.
חיבור וחיסור במערכת המספרים המצרית נעשו באופן פשוט ביותר. חיבור של שני מספרים נעשה ע"י צירוף של הסימנים המופיעים בשני המספרים, ולאחר מכן החלפה של עשרה סימנים מאותו סוג בסימן בעל ערך גבוה יותר. לדוגמא נראה כיצד המצרים חיברו את המספרים 345 ו- 678 :

תחילה מצרפים את כל הסימנים המרכיבים את 345 ו- 678, והתוצאה היא 13 מקלות (אחדות), 11 פרסות (עשרות), ו- 9 חבלים (מאות). לאחר מכן מחליפים 10 מקלות בפרסה ו- 10 פרסות בחבל. לבסוף מחליפים 10 חבלים בפרח לוטוס אחד.
המספר המתקבל בסוף הוא 1023 = 3 + 10 ∙ 2 + 1000 , וזהו אכן הסכום של 345 ו- 678.
להלן קישור לאתר שבו תוכלו לתרגם מספרים בכתיבה שלנו למספרים בכתיבה המצרית ולהיפך:http://www.psinvention.com/zoetic/tr_egypt.htm
ראשית המתמטיקה - פרקים נוספים:
ראשית המתמטיקה
עצם האישנגו
מערכות מספרים קדומות
מערכת המספרים הרומאית
מערכות מספרים פוזיציונליות (מיקומיות)
מערכת המספרים הבבלית
מערכת המספרים ההודו-ערבית
| ביבליוגרפיה: | ||||||||||||||
|
 |
 |
חזרה3 |
 |
הדפסה | ||||||
| החומר במאגר זה הינו לשימוש פרטי ולשימושם של מורים ותלמידים לצרכים לימודיים בלבד. אין להפיץ, להעתיק, לשדר או לפרסם חומר כלשהו מתוך המאגר, ללא הסכמה מראש ובכתב של בעלי זכויות היוצרים השונים, המצויינים בתחתית כל פריט. | |||||||
|
|||||||
| החומר במאגר זה הינו לשימוש פרטי ולשימושם של מורים ותלמידים לצרכים לימודיים בלבד. אין להפיץ, להעתיק, לשדר או לפרסם חומר כלשהו מתוך המאגר, ללא הסכמה מראש ובכתב של בעלי זכויות היוצרים השונים, המצויינים בתחתית כל פריט. |